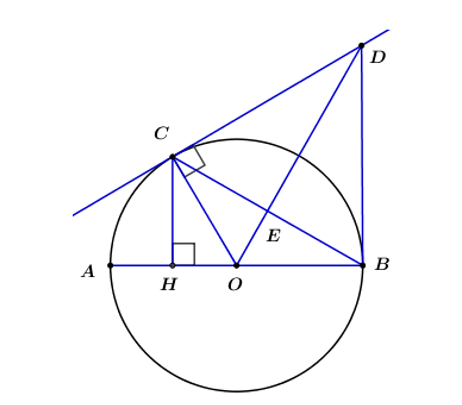
Cho (O) đường kính AB. Lấy C thuộc (O), gọi E là trung điểm BC. Tiếp tuyến tại C của (O) cắt OE ở D. Chứng minh: ΔACB vuông và OE ⊥ BC.
20
27/09/2024
Cho (O) đường kính AB. Lấy C thuộc (O), gọi E là trung điểm BC. Tiếp tuyến tại C của (O) cắt OE ở D. Chứng minh: ΔACB vuông và OE ⊥ BC.
Trả lời
Xét đường tròn (O) có AB là đường kính và ΔABC nội tiếp đường tròn (O)
hay ΔABC vuông tại C.
Ta có: OC = OB (do cùng bằng bán kính)
Þ O cách đều hai điểm C và B,
Þ O nằm trên trung trực của BC.
Lại có: EC = EB (do E là trung điểm của BC)
Þ E cách đều hai điểm B và C
Þ E nằm trên trung trực của BC.
Ta có E và O đều nằm trên đường trung trực của đoạn BC
Þ OE là trung trực của đoạn BC.
Vậy OE ⊥ BC.