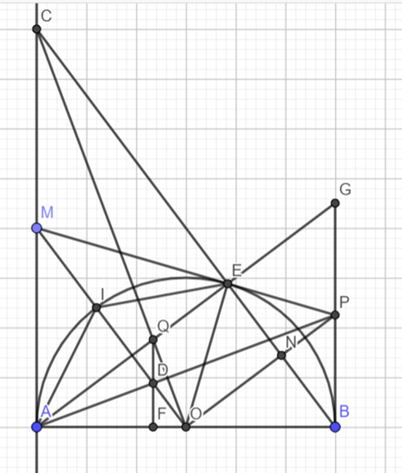
Cho nửa đường tròn tâm O với bán kính R, đường kính AB. Trên nửa mặt phẳng
Cho nửa đường tròn tâm O với bán kính R, đường kính AB. Trên nửa mặt phẳng bờ là đường thẳng AB chứa nửa đường tròn, kẻ tiếp tuyến Ax tại A của nửa đường tròn. Xét điểm M thay đổi trên Ax, không trùng với A. Gọi E là điểm đối xứng với A qua OM.
a) Chứng minh rằng ME là một tiếp tuyến của nửa đường tròn (O)
b) Đoạn OM cắt nửa đường tròn (O) tại I. Chứng minh rằng I là tâm đường tròn nội tiếp của tam giác AME
c) Gọi N là trung điểm EB. Tia ME cắt ON tại P. Hãy xác định vị trí của điểm M trên tia Ax để diện tích tam giác OMP đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó theo R.
c) Gọi C là giao điểm của BE và tia Ax, OC cắt AE tại Q. Kẻ đường thẳng qua Q và song song với Ax, cắt OM tại D. Chứng minh rằng A, D, P thẳng hàng.