Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên đường tròn (M khác A; B) vẽ tiếp tuyến với nửa đường tròn, cắt Ax và

Trả lời

Lời giải

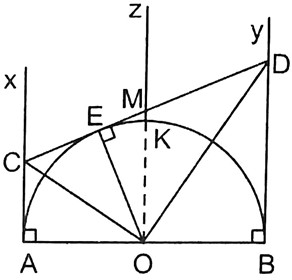
Theo tính chất của hai tiếp tuyến cắt nhau ta có:

• OC là tia phân giác của \[\widehat {AOM}\];

• OD và tia phân giác của \[\widehat {BOM}\].

Khi đó, OC và OD là các tia phân giác của hai góc kề bù \[\widehat {AOM}\] và \[\widehat {BOM}\].

Do đó OC ⊥ OD.

Vậy \[\widehat {COD} = 90^\circ \] (đpcm)

b) Ta có: AC = CM, BD = DM nên AC . BD = CM . MD.

Xét ΔCOD vuông tại O, ta có:

CM . MD = OM² = R² (R là bán kính đường tròn O).

Vậy AC . BD = R² (không đổi).