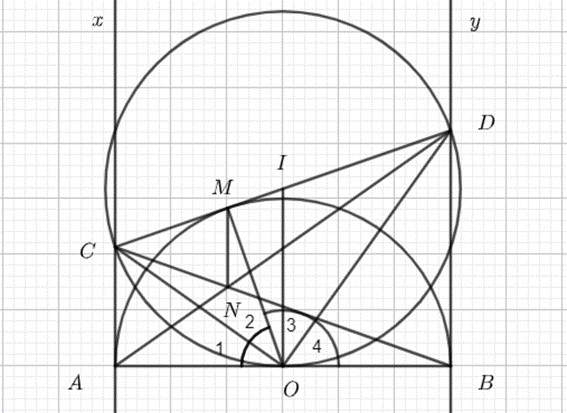
a) Do CA và CM là hai tiếp tuyến cắt nhau nên CA = CM
Do DM và DB là hai tiếp tuyến cắt nhau nên DM = DB
Suy ra CD = CM + MD = CA + DB (đpcm)
Ta có \(\widehat {{O_1}} = \widehat {{O_2}}\) (tính chất 2 tiếp tuyến cắt nhau)
và \(\widehat {{O_3}} = \widehat {{O_4}}\) (tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow \widehat {COD} = \widehat {{O_2}} + \widehat {{O_3}} = \frac{{\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}}}}{2} = 90^\circ \) (đpcm)
b) ΔCOD vuông tại O có đường cao OM
Áp dụng hệ thức lượng ta có:
OM2 = CM.MD Þ R2 = CA.DB (đpcm)
c) Gọi I là trung điểm của CD thì OI là đường trung bình của hình thang ACDB
Þ IO // AC // BD
Þ IO ^ AB mà OI = IC = ID
Vậy I là tâm đường tròn đường kính CD
Hay AB là tiếp tuyến của đường tròn (I; IC).
d) Do Ax và By là hai tiếp tuyến của (O)
Nên Ax // By (vì cùng ^ AB)
Hay AC // DB
Theo định lý Ta-let ta có:
\(\frac{{NA}}{{ND}} = \frac{{NC}}{{NB}} = \frac{{AC}}{{BD}}\)
Mà AC = CM và BD = DM Þ \(\frac{{AC}}{{BD}} = \frac{{CM}}{{DM}}\)
\( \Rightarrow \frac{{NA}}{{ND}} = \frac{{CM}}{{DM}}\)
Hay \(\frac{{NA + ND}}{{ND}} = \frac{{CM + DM}}{{DM}}\)
\( \Leftrightarrow \frac{{AD}}{{ND}} = \frac{{CD}}{{DM}} \Leftrightarrow \frac{{ND}}{{AD}} = \frac{{DM}}{{CD}}\)
Þ MN // AC (định lý Ta-let) (đpcm).