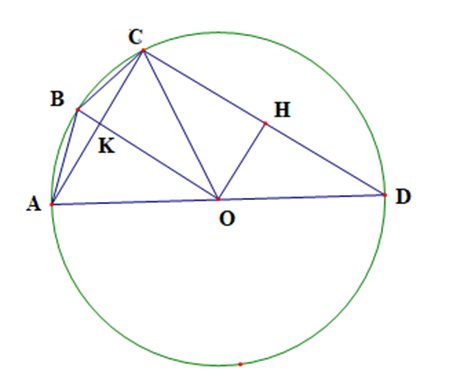
Từ O kẻ OH vuông góc với CD. Nối O với B, OB cắt AC tại K

Suy ra OB ⊥ AC

Vì tam giác ACD nội tiếp (O) đường kính AD

Nên $\widehat {ACD} = 90^\circ$

Xét tứ giác OHCK có $\widehat {OKC} = \widehat {KCH} = \widehat {OHC} = 90^\circ$

Suy ra OHCK là hình chữ nhật

Do đó OK = CH = $\frac{1}{2}$CD = 3, OH = CK = $\sqrt {O{C^2} - O{K^2}} = \sqrt {{R^2} - 9}$        (1)

Xét tam giác BCK vuông ở K có

CK = $\sqrt {B{C^2} - B{K^2}} = \sqrt {{{\left( {2\sqrt 5 } \right)}^2} - {{\left( {R - 3} \right)}^2}}$                                             (2)

Từ (1) và (2) ta có

$\sqrt {{R^2} - 9} = \sqrt {{{\left( {2\sqrt 5 } \right)}^2} - {{\left( {R - 3} \right)}^2}}$

$\Leftrightarrow \sqrt {{R^2} - 9} = \sqrt {20 - {R^2} + 6{\rm{R}} - 9}$

$\Leftrightarrow \sqrt {{R^2} - 9} = \sqrt {11 - {R^2} + 6{\rm{R}}}$

⟺ ${R^2} - 9 = 11 - {R^2} + 6{\rm{R}}$

⟺ 2R² – 6R – 20 = 0

⟺ $\left[ \begin{array}{l}R = 5\\R = - 2\end{array} \right.$

Vậy bán kính đường tròn là 5 cm.