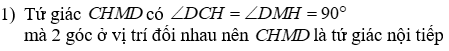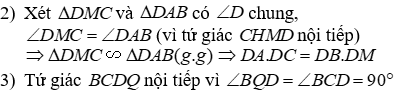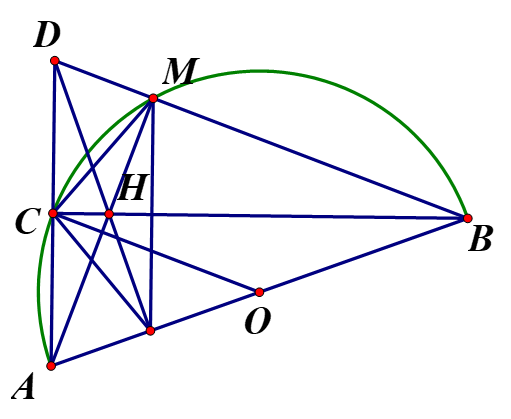
Cho nửa đường tròn \(\left( O \right)\), đường kính \(AB.\)Lấy \(M\)bất kỳ thuộc nửa đường tròn (không trùng với \(A,B)\)và C là điểm chính giữa cung \(AM.\)Gọi \(D\)là giao điểm của \(AC\)và \(BM;H\)là giao điểm của \(AM\)và \(BC\)

1)    Chứng minh tứ giác \(CHMD\)nội tiếp

2)    Chứng minh \(DA.DC = DB.DM\)

3)    Gọi \(Q\)là giao điểm của \(DH\)và \(AB.\)Chứng minh khi điểm \(M\)di chuyển trên nửa đường tròn thì đường tròn ngoại tiếp \(\Delta CMQ\)luôn đi qua một điểm cố định.