Cho nửa đường tròn (O), đường kính AB. Kẻ 2 tiếp tuyến Ax, By (Ax, By và nửa đường tròn
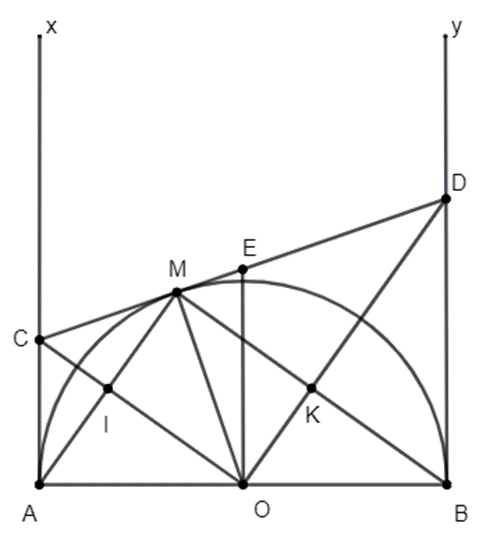
Cho nửa đường tròn (O), đường kính AB. Kẻ 2 tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi C là một điểm thuộc tia Ax, kẻ tiếp tuyến CM với nửa đường tròn (M là tiếp điểm). CM cắt By tại D. Gọi I là giao điểm của OC và AM, K là giao điểm của OD và MB.
a) Tính ^COD.
b) Tứ giác OIMK là hình gì?
c) Chứng minh AC.BD không đổi khi C di chuyển trên Ax.
d) Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.