Cho nửa đường tròn (O), đường kính AB; Ax là tiếp tuyến của nửa đường tròn. Trên nửa đường tròn lấy điểm D (D khác A, B). Tiếp tuyến tại D của (O) cắt Ax ở S. a) Chứng minh SO // BD. b) BD
41
19/05/2024
Cho nửa đường tròn (O), đường kính AB; Ax là tiếp tuyến của nửa đường tròn. Trên nửa đường tròn lấy điểm D (D khác A, B). Tiếp tuyến tại D của (O) cắt Ax ở S.
a) Chứng minh SO // BD.
b) BD cắt AS ở C. Chứng minh SA = SC.
c) Kẻ DH vuông góc với AB; DH cắt BS tại E. Chứng minh E là trung điểm của DH.
Trả lời
Lời giải
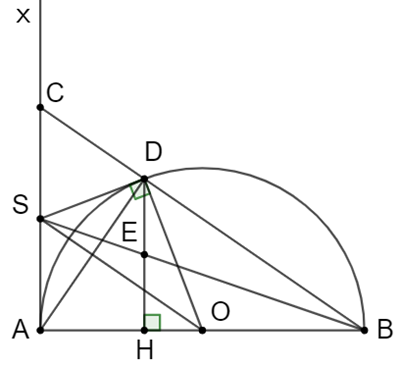
a) Ta có: SA và SD là hai tiếp tuyến của (O) và cắt nhau tại S Þ SA = SD.
Mà OA = OD (Bán kính của đường tròn (O)).
Khi đó SO là đường trung trực của đoạn thẳng AD Þ SO ^ AD.
Tam giác ABD nội tiếp đường tròn (O) nên suy ra AD ^ BD.
Vậy suy ra SO // BD (đpcm).
b) Xét ∆ABC có:
O là trung điểm của AB;
SO // BD (cmt).
Suy ra SO là đường trung bình của ∆ABC.
Do đó S là trung điểm của AC.
Vậy SA = SC (đpcm).
c) Do AC ^ AB và DH ^ AB nên suy ra AC // DH
Xét ∆BSC có ED // SC. Theo định lý Ta-lét, ta có: \(\frac{{BE}}{{BS}} = \frac{{ED}}{{SC}}\) (1)
Xét ∆BSA có EH // SA. Theo định lý Ta-lét, ta có: \(\frac{{BE}}{{BS}} = \frac{{EH}}{{SA}}\) (2)
Từ (1) và (2) \( \Rightarrow \frac{{ED}}{{SC}} = \frac{{EH}}{{SA}}\).
Mà SC = SA Þ ED = EH.
Vậy E là trung điểm của DH.

