Cho nửa đường tròn đường kính AB, C là một điểm thuộc nửa đường tròn. Vẽ dây BD là phân giác của góc ABC, BD cắt AC tại E, AD cắt BC tại G. H là điểm đối xứng với E qua D. Chọn câu đúng: A.
82
18/05/2024
Cho nửa đường tròn đường kính AB, C là một điểm thuộc nửa đường tròn. Vẽ dây BD là phân giác của \[\widehat {ABC}\], BD cắt AC tại E, AD cắt BC tại G. H là điểm đối xứng với E qua D. Chọn câu đúng:
A. AH là tiếp tuyến của đường tròn đường kính AB;
B. HG là tiếp tuyến của đường tròn đường kính AB;
C. \(\widehat {ADB} = 90^\circ \);
D. Cả A và C đều đúng.
Trả lời
Lời giải
Đáp án đúng là: D
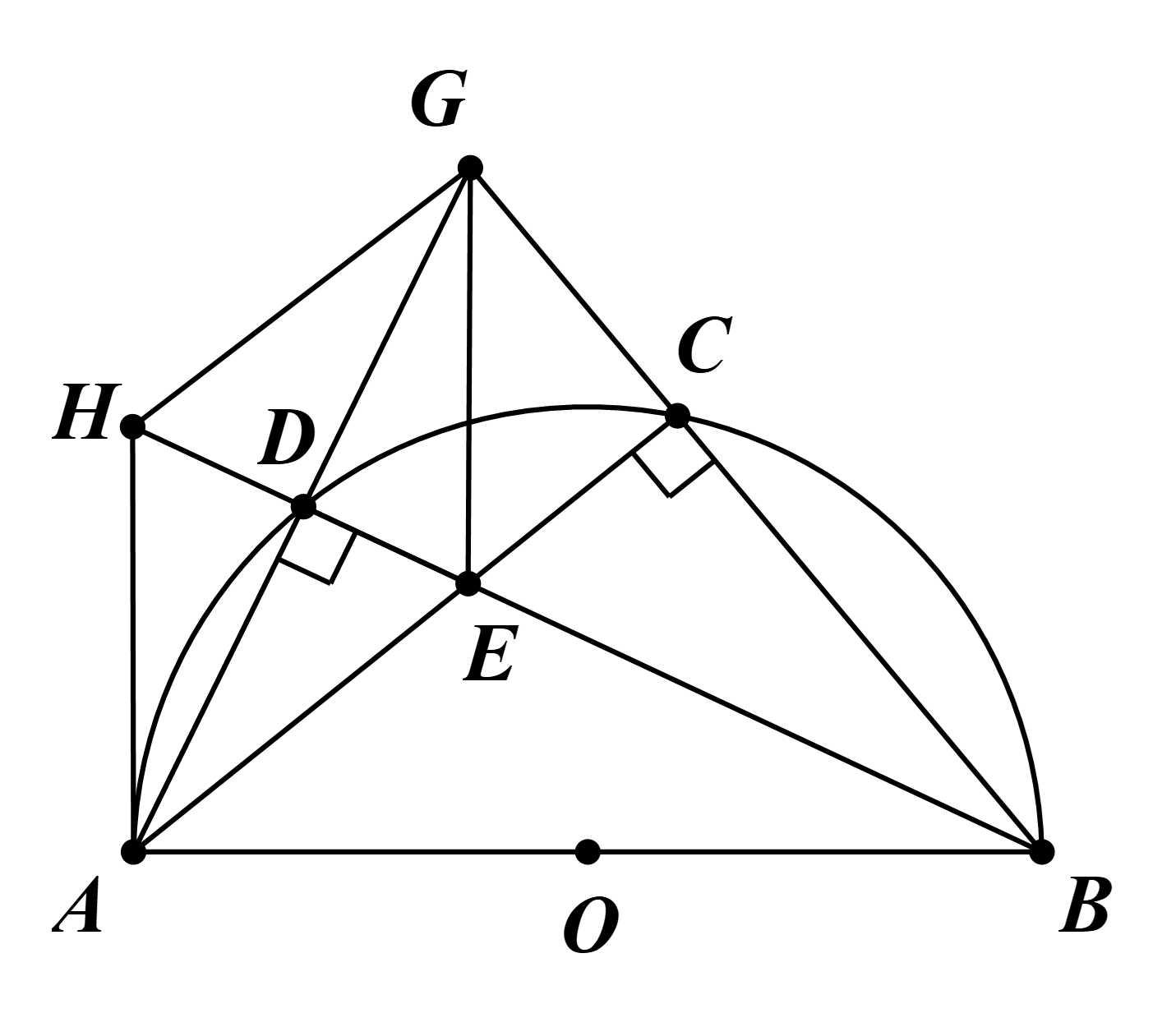
Ta có \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Suy ra BD ⊥ AG.
Tam giác AGB có BD vừa là đường cao vừa là đường phân giác.
Suy ra tam giác AGB cân tại B.
Do đó BD cũng là đường trung tuyến của tam giác AGB.
Vì vậy D là trung điểm của AG.
Mà D cũng là trung điểm của HE (do H là điểm đối xứng với E qua D) và AG ⊥ HE (chứng minh trên).
Vậy tứ giác AHGE là hình thoi.
Ta có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Suy ra CA ⊥ BG.
Tam giác AGB có hai đường cao AC, BD cắt nhau tại E.
Suy ra E là trực tâm của tam giác AGB.
Do đó GE ⊥ AB.
Mà GE // AH (do tứ giác AHGE là hình thoi).
Suy ra AH ⊥ AB.
Vậy AH là tiếp tuyến của đường tròn đường kính AB.
Do đó ta chọn phương án D.
