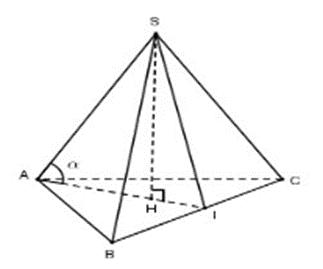
Cho một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với
Cho một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với mặt phẳng đáy một góc α. Thể tích của hình chóp là:
A. \(\frac{3}{4}{b^3}{\rm{co}}{{\rm{s}}^2}\alpha \sin \alpha \);
B. \(\frac{{\sqrt 3 }}{4}{b^3}{\rm{co}}{{\rm{s}}^2}\alpha \sin \alpha \);
C. \(\frac{3}{4}{b^3}{\rm{cos}}\alpha {\sin ^2}\alpha \);
D. \(\frac{{\sqrt 3 }}{4}{b^3}{\rm{cos}}\alpha \sin \alpha \).