Cho ΔMNP có I là trung điểm cạnh NP. Trên tia đối của IM lấy D sao cho IM = ID.
a) Chứng minh ΔMIN = ΔDIP.
b) Chứng minh MN // DP.
c) Gọi H là trung điểm MN, vẽ E sao cho H là trung điểm của PE. Chứng minh N là trung điểm của ED.
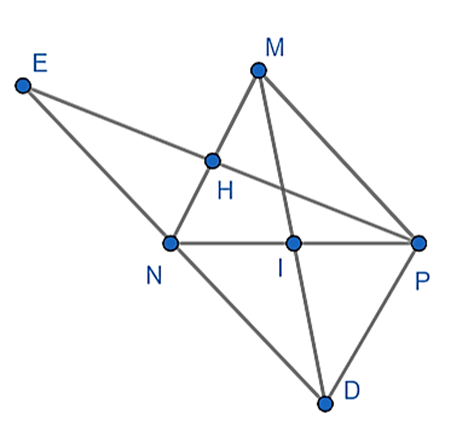
a) Xét ΔMIN và ΔDIP có:
IM = ID (giả thiết)
^MIN=^PID(đối đỉnh)
NI = IP
Suy ra: ΔMIN = ΔDIP (c.g.c)
b) Theo phần a có ΔMIN = ΔDIP nên MN = PD và ^MNI=^IPD(hai cạnh và hai góc tương ứng)
Mà hai góc ^MNI,^IPD ở vị trí so le trong nên MN // PD
c) Xét ΔMIP và ΔDIN có:
MI = ID
^MIP=^NID(đối đỉnh)
IP = IN
Suy ra: ΔMIP = ΔDIN (c.g.c)
⇒ ^IND=^IPM(hai góc tương ứng)
Suy ra: ND // MP (*) và ND = MP (1)
Xét ΔEHN và ΔPHM có:
HE = HP (giả thiết)
^EHN=^MHP(đối đỉnh)
HM = HN (giả thiết)
Suy ra: ΔEHN = ΔPMH (c.g.c)
⇒ ^HMP=^HNE(hai góc tương ứng) và EN = MP (2)
Mà hai góc ^MNI,^IPD ở vị trí so le trong nên NE // MP (**)
Từ (*) và (**) suy ra: ND trùng NE hay E, N, D thẳng hàng
Từ (1) và (2) suy ra: NE = ND
Vậy N là trung điểm ED.