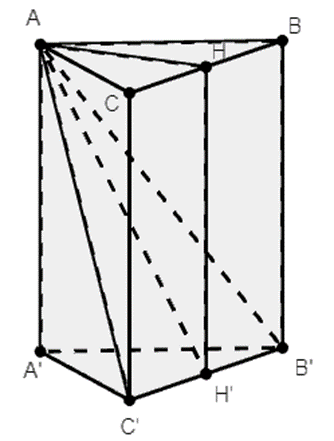
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt phẳng (ABC) một góc 60°. Thể tích khối lăng trụ ABC.A'B'C' bằng
A. \(\frac{{{a^3}\sqrt 3 }}{2}\);
B. \(\frac{{3{a^3}\sqrt 3 }}{4}\);
C. \(\frac{{{a^3}\sqrt 3 }}{8}\);
D. \(\frac{{3{a^3}\sqrt 3 }}{8}\).
Đáp án đúng là: D
Gọi H, H' lần lượt là trung điểm của BC, B'C'.
Do lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a nên \(AH = \frac{{a\sqrt 3 }}{2}\)
Và \({S_{\Delta A'B'C'}} = \frac{{{a^2}\sqrt 3 }}{4}\).
Ta có: ((AB’C”), (ABC)) = (AH, AH’) \( = \widehat {H'AH} = 60^\circ \).
Xét tam giác H'HA vuông tại H có:
\(\tan 60^\circ = \frac{{H'H}}{{AH}} \Leftrightarrow H'H = AH.\tan 60^\circ = \frac{{a\sqrt 3 }}{2}.\sqrt 3 = \frac{3}{2}a\).
Mà A'A=H'H nên \(A'A = \frac{3}{2}a\).
Vậy \({V_{ABC.A'B'C'}} = A'A.{S_{\Delta A'B'C'}} = \frac{3}{2}a.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{8}{a^3}\).