Cho khối lăng trụ tam giác đều ABC.A'B'C'. Gọi M là trung điểm cạnh AA'. Mặt phẳng
Cho khối lăng trụ tam giác đều ABC.A'B'C'. Gọi M là trung điểm cạnh AA'. Mặt phẳng (MBC) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó.
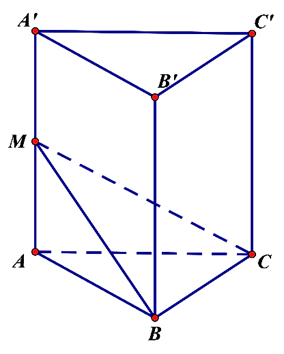
Mặt phẳng (MBC) chia khối lăng trụ thành hai phần M.ABC và MA'B'C'BC. Ta có:
\({V_{M.ABC}} = \frac{1}{3}\,.\,\frac{1}{2}h\,.\,{S_{ABC}} = \frac{1}{6}{V_{ABC.A'B'C'}}\)
Suy ra \({V_{MA'B'C'BC}} = \frac{5}{6}{V_{ABC.A'B'C'}}\)
Tỉ số thể tích cua hai phần đó bằng:
\(\frac{{{V_{M.ABC}}}}{{{V_{MA'B'C'BC}}}} = \frac{{\frac{1}{6}{V_{ABC.A'B'C'}}}}{{\frac{5}{6}{V_{ABC.A'B'C'}}}} = \frac{1}{5}\).