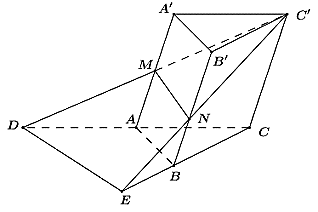
Ta có: V_AMDBNE = V_C'.CDE − V_CC'ABMN = V_C'.CDE − (V − V_C'.A'B'NM)

$\frac{S_{CDE}}{S_{ABC}}=\frac{CD}{CA}.\frac{CE}{CB}$

Áp dụng định lí Ta-lét ta có:

$\frac{DA}{DC}=\frac{AM}{CC\text{'}}=\frac{1}{2}\Rightarrow \frac{CD}{CA}=2$

$\frac{EB}{EC}=\frac{BN}{CC\text{'}}=\frac{1}{3}\Rightarrow \frac{CE}{CB}=\frac{3}{2}$

$\Rightarrow \frac{S_{CDE}}{S_{ABC}}=\frac{CD}{CA}.\frac{CE}{CB}=2.\frac{3}{2}=3$

Lại có chóp C'.CDE và lăng trụ có cùng chiều cao.

$\Rightarrow \frac{V_{C\text{'}.CDE}}{V}=\frac{1}{3}\frac{S_{CDE}}{S_{ABC}}=1\Rightarrow V_{C\text{'}.CDE}=V$

Ta có:

$\frac{S_{A\text{'}B\text{'}NM}}{S_{ABB\text{'}A\text{'}}}=\frac{\frac{1}{2}\left(A\text{'}M+B\text{'}N\right).d\left(A\text{'};BB\text{'}\right)}{BB\text{'}.d\left(A\text{'};BB\text{'}\right)}$

$=\frac{\frac{1}{2}\left(\frac{1}{2}BB\text{'}+\frac{2}{3}BB\text{'}\right)}{BB\text{'}}=\frac{7}{12}$

$\Rightarrow \frac{V_{C\text{'}.A\text{'}B\text{'}NM}}{V_{C\text{'}.ABB\text{'}A\text{'}}}=\frac{S_{A\text{'}B\text{'}NM}}{S_{ABB\text{'}A\text{'}}}=\frac{7}{12}$

$\Rightarrow V_{C\text{'}.A\text{'}B\text{'}NM}=\frac{7}{12}{V}_{C\text{'}.ABB\text{'}A\text{'}}$

Mà  $V_{C\text{'}.ABB\text{'}A\text{'}}=\frac{2}{3}V\Rightarrow V_{C\text{'}.A\text{'}B\text{'}NM}=\frac{7}{12}.\frac{2}{3}V=\frac{7}{18}V$

Vậy  $V_{AMDBNE}=V-\left(V-\frac{7}{18}V\right)=\frac{7}{18}V$ hay  $\frac{V_{AMDBNE}}{V}=\frac{7}{18}$.