Cho khối chóp S.ABC có đáy là tam giác vuông tại B , $\widehat{SAB}=\widehat{SCB}=90°$ . AB = a , BC = 2a . Biết rằng góc giữa đường thẳng SB và mặt phẳng đáy bằng 60°. Thể tích khối chóp đã cho bằng?

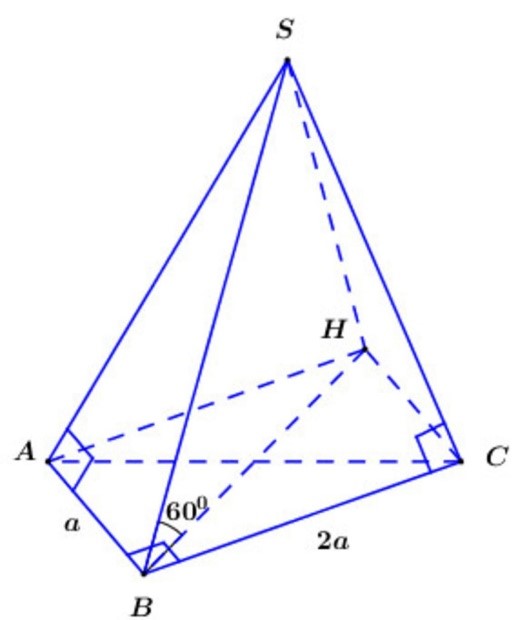
Gọi H là hình chiếu vuông góc của S lên (ABC)

Ta có:

 $\left\{\begin{array}{l}BC\perp SC\\ BC\perp SH\left(SH\perp \left(ABC\right)\right)\end{array}\right.$⇒ BC ⊥ (SCH) ⇒ BC ⊥ CH

$\left\{\begin{array}{l}{\rm A}{\rm B}\perp SA\\ {\rm A}{\rm B}\perp SH\left(SH\perp \left(ABC\right)\right)\end{array}\right.$ ⇒ AB ⊥ (SAH) ⇒ AB ⊥ AH

⇒ ABCH là hình chữ nhật (tứ giác có 3 góc vuông)

Vì SH ⊥ (ABC) nên HB là hình chiếu vuông góc của SB lên (ABC)

⇒ $\widehat{SB;\left(ABC\right)}=\widehat{SB;HB}=\widehat{SBH}=60°$

Áp dụng định lý Pitago ta có: AC = $\sqrt{A{B}^2+B{C}^2}=a\sqrt{5}$

Lại có: ABCH là hình vuông nên BH = AC = $a\sqrt{5}$

Xét tam giác vuông SBH có: SH = BH. tan30° = $a\sqrt{15}$

Vậy V_S.ABC = $\frac{1}{3}$  SH.S_ABC = $\frac{1}{3}$ . $a\sqrt{15}$.a.2a = $\frac{a^3\sqrt{15}}{3}$