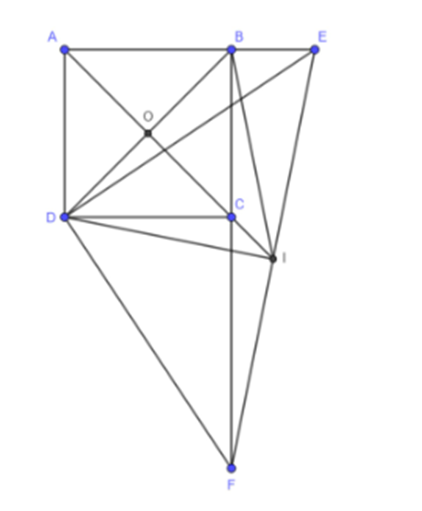
a) Vì ABCD là hình vuông nên AB = BC = CD = DA.

Xét DDAE và DDCF có

AD = CD (chứng minh trên);

$\widehat {DA{\rm{E}}} = \widehat {DCF}\left( { = 90^\circ } \right)$;

AE = CF (giả thiết).

Suy ra DDAE = DDCF (c.g.c)

Do đó DE = DF (1) và $\widehat {A{\rm{D}}E} = \widehat {C{\rm{D}}F}$                          

Ta có $\widehat {A{\rm{D}}E} + \widehat {C{\rm{DE}}} = 90^\circ$

Suy ra $\widehat {C{\rm{D}}F} + \widehat {C{\rm{DE}}} = 90^\circ$

Hay $\widehat {E{\rm{D}}F} = 90^\circ$                    (2)

Từ (1) và (2) suy ra tam giác EDF vuông cân tại D.

b) Xét tam giác EBF vuông tại B có BI là trung tuyến, suy ra $BI = \frac{1}{2}EF$

Xét tam giác EDF vuông tại D có BI là trung tuyến, suy ra $DI = \frac{1}{2}EF$

Do đó BI = DI.

c) Xét hình chữ nhật ABCD có O là giao điểm của hai đường chéo AC và BD

Suy ra O là trung điểm của BD

Do đó O thuộc đường trung trực của BD

Vì BI = DI nên I thuộc đường trung trực của BD

Vì CD = CB nên C thuộc đường trung trực của BD

Suy ra O, I, C cùng thuộc đường trung trực của BD.

Vậy O, I, C thẳng hàng.