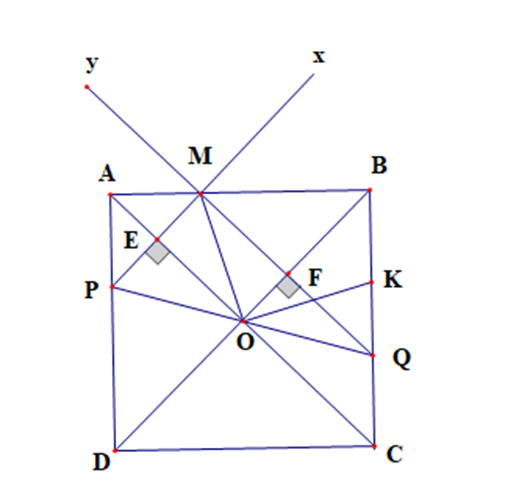
a) Vì ABCD là hình vuông tâm O
Nên OA = OB = OC = OD, AB = BC = CD = DA, AD // BC
Suy ra \(\widehat {DAC} = \widehat {ACB}\) (hai góc so le trong)
Xét tam giác AOP và tam gíc COQ có
\(\widehat {DAC} = \widehat {ACB}\) (chứng minh trên)
OA = OC (chứng minh trên)
\(\widehat {AOP} = \widehat {COQ}\) (hai góc đối đỉnh)
Do đó ΔAOP = ΔCOQ (g.c.g)
Suy ra AP = CQ (hai cạnh tương ứng)
b) Vì AB = AD nên tam giác ABD cân tại A
Mà AO là đường trung tuyến
Suy ra AO là đường cao
Hay AO ⊥ BD
Xét tứ giác OEMF có
\(\widehat {OEM} = \widehat {EOF} = \widehat {OFM} = 90^\circ \)
Suy ra OEMF là hình chữ nhật
c) Vì OEMF là hình chữ nhật
Nên \[\widehat {FME} = 90^\circ \]
Hay tam giác PMQ vuông tại M
Mà MO là trung tuyến
Suy ra OM = OP = OQ
Do đó tam giác POM cân tại O
Lại có OE là đường cao nên OE là phân giác của \(\widehat {POM}\)
Suy ra \(\widehat {POE} = \widehat {EOM}\)
Xét tam giác AOP và tam giác AOM có
AO là cạnh chung
\(\widehat {POE} = \widehat {EOM}\) (chứng minh trên)
OM = OP (chứng minh trên)
Suy ra △AOP = △AOM (c.g.c)
Do đó \(\widehat {AP{\rm{O}}} = \widehat {AM{\rm{O}}}\) (hai góc tương ứng)
Ta có OM = OQ
Do đó tam giác QOM cân tại O
Lại có OF là đường cao nên OF là phân giác của \(\widehat {QOM}\)
Suy ra \(\widehat {QOF} = \widehat {FOM}\)
Xét tam giác BOQ và tam giác BOM có
BO là cạnh chung
\(\widehat {QOF} = \widehat {FOM}\) (chứng minh trên)
OM = OQ (chứng minh trên)
Suy ra △ BOQ = △BOM (c.g.c)
Do đó \(\widehat {{\rm{BQO}}} = \widehat {BM{\rm{O}}}\) (hai góc tương ứng)
Vì AD // BC nên \(\widehat {AP{\rm{O}}} + \widehat {BQO} = 180^\circ \)
Mà \(\widehat {{\rm{BQO}}} = \widehat {BM{\rm{O}}}\), \(\widehat {AP{\rm{O}}} = \widehat {AM{\rm{O}}}\)
Suy ra \(\widehat {AM{\rm{O}}} + \widehat {BMO} = 180^\circ \)
Hay \(\widehat {AMB} = 180^\circ \)
Do đó A, M, B thẳng hàng
Vậy M thuộc cạnh AB
d) Ta có: AP = AD – DP, BK = BC – CK
Mà AD = BC, PD = CK
Suy ra AP = BK
Vì ABCD là hình vuông tâm O
Nên \(\widehat {DAO} = \widehat {OBC} = 45^\circ \)
Xét tam giác POA và tam giác KOB có
OA = OB
\(\widehat {DAO} = \widehat {OBC}\) (chứng minh trên)
PA = BK (chứng minh trên)
Suy ra △POA = △KOB (c.g.c)
Do đó \(\widehat {POA} = \widehat {K{\rm{OB}}}\) (hai góc tương ứng)
Mà \(\widehat {POA} = \widehat {{\rm{AOM}}}\)
Nên \(\widehat {KOB} = \widehat {{\rm{AOM}}}\)
Mặt khác \(\widehat {AOM} + \widehat {{\rm{MOB}}} = \widehat {AOB} = 90^\circ \) (hai góc kề bù)
Suy ra \(\widehat {BOK} + \widehat {{\rm{MOB}}} = 90^\circ \)
Hay \(\widehat {MOK} = 90^\circ \)
Vậy \(\widehat {MOK} = 90^\circ \).