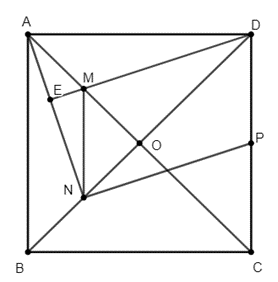
Lời giải
a) Vì MN là đường trung bình của ∆OAB nên MN // AB.
Suy ra AM = NB = \(\frac{1}{2}OA = \frac{1}{2}OB\).
Do đó tứ giác MNBA là hình thang cân.
b) Ta có MN // AB nên MN // DP
Do đó MN = \(\frac{1}{2}AB = \frac{1}{2}DC = DP\).
Vậy tứ giác MNPD là hình bình hành.
c) Xét ∆DMB có MO vừa là đường trung tuyến vừa là đường cao.
Suy ra DMB là tam giác cân.
Do đó \(\widehat {MBD} = \widehat {MDB}\) (1)
Dễ thấy: ∆OAN = ∆OBM suy ra \(\widehat {MBO} = \widehat {OAN}\) (2)
Từ (1) và (2) suy ra \(\widehat {OAN} = \widehat {MDB}\).
Mà \(\widehat {DNP} = \widehat {MDB}\) (hai góc so le trong)
Suy ra \(\widehat {DNP} = \widehat {OAN}\).
Xét ∆OAN có \(\widehat {OAN} + \widehat {ONA} = 90^\circ \)
\( \Rightarrow \widehat {DNP} + \widehat {ONA} = 90^\circ \)\( \Rightarrow \)NP\( \bot \)AN.
Mà DM // ND suy ra DM\( \bot \)AN.