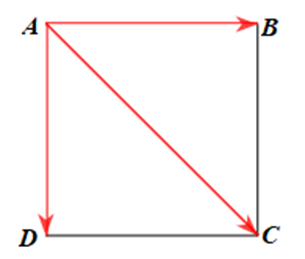
Cho hình vuông ABCD cạnh a. Tính vecto AB + vecto AC + vecto AD A. 3a
Cho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{\rm{D}}} } \right|\).
A. 3a;
B. \(\left( {2 + \sqrt 2 } \right)\)a;
C. a\(\sqrt 2 \);
D. 2a\(\sqrt 2 \).