Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm A1, A2 sao cho AA1 = A1A2 = A2S. Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua A1, A2. Mặt phẳng (P) cắt cá

Trả lời

Lời giải:

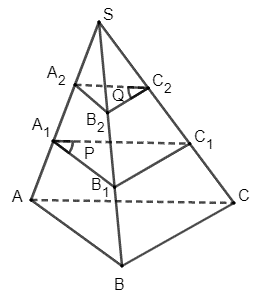
Vì hai mặt phẳng (P) và (Q) song song với mặt phẳng (ABC) nên (P) // (Q), do đó ba mặt phẳng (ABC), (P) và (Q) đôi một song song. Theo định lí Thalés trong không gian, ta suy ra \(\frac{{{A_2}{A_1}}}{{A{A_1}}} = \frac{{{B_2}{B_1}}}{{B{B_1}}} = \frac{{{C_2}{C_1}}}{{C{C_1}}}\).

Mà AA₁ = A₁A₂ nên \[\frac{{{A_2}{A_1}}}{{A{A_1}}} = 1\], suy ra \(\frac{{{A_2}{A_1}}}{{A{A_1}}} = \frac{{{B_2}{B_1}}}{{B{B_1}}} = \frac{{{C_2}{C_1}}}{{C{C_1}}} = 1\), do đó BB₁ = B₁B₂ và CC₁ = C₁C₂.

Sử dụng định lí Thalés ta cũng chứng minh được \(\frac{{{A_2}S}}{{{A_2}{A_1}}} = \frac{{{B_2}S}}{{{B_2}{B_1}}} = \frac{{{C_2}S}}{{{C_2}{C_1}}}\).

Mà A₁A₂ = A₂S nên \(\frac{{{A_2}S}}{{{A_2}{A_1}}} = 1\), suy ra \(\frac{{{A_2}S}}{{{A_2}{A_1}}} = \frac{{{B_2}S}}{{{B_2}{B_1}}} = \frac{{{C_2}S}}{{{C_2}{C_1}}} = 1\), do đó B₁B₂ = B₂S và C₁C₂ = C₂S.

Vậy BB₁ = B₁B₂ = B₂S và CC₁ = C₁C₂ = C₂S.