Cho hình tứ diện ABCD. Gọi I, J lần lượt thuộc cạnh AD, BC sao cho IA = 2ID, JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Khẳng định nào đúng?

A. CD cắt (P); 

B. (P) // CD; 

Đáp án đúng là: B

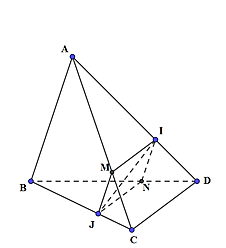
Kẻ MJ // AB, M Î AC và NI // AB, N Î BD.

Suy ra M, N, I, J đồng phẳng và (MINJ) º (P)

Thiết diện của mặt phẳng (P) và tứ diện ABCD là tứ giác MINJ, có:

Do  $\frac{AM}{AC}=\frac{AI}{AD}=\frac{2}{3}$ nên suy ra MI // CD

Mà MI Ì (P) nên suy ra (P) // CD.

Do đó CD không thể cắt (P).

Ta có MI // CD mà IJ cắt MI tại I và MI, IJ Ì (P) nên suy ra IJ không song song với CD.

Lại có:  $\frac{DI}{DA}=\frac{DN}{DB}=\frac{1}{3}$ nên suy ra IN // AB

Mà IJ cắt IN tại I và IN, IJ Ì (P) nên suy ra IJ không song song với AB.