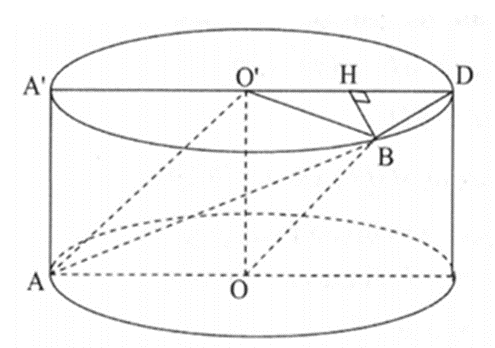
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB = 2a. Thể tích khối tứ diện OO'AB theo a là:
A. \(V = \frac{{\sqrt 3 {a^3}}}{8}\)
B. \(V = \frac{{\sqrt 3 {a^3}}}{4}\)
C. \(V = \frac{{\sqrt 3 {a^3}}}{6}\)
D. \(V = \frac{{\sqrt 3 {a^3}}}{{12}}\).