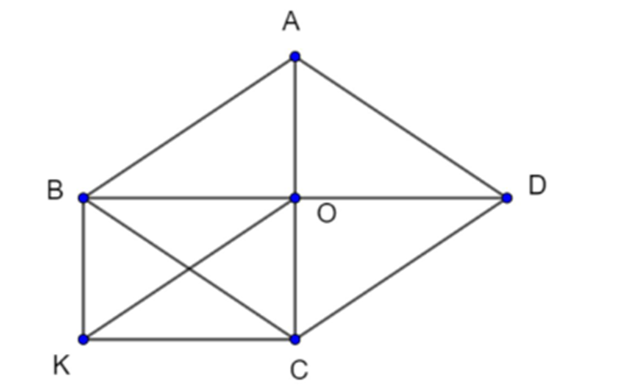
Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Vẽ đường thẳng qua
Cho hình thoi ABCD, gọi O là giao điểm của hai đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, hai đường thẳng đó cắt nhau tại K.
a) Tứ giác OBKC là hình gì ? Vì sao ?
b) Chứng minh rằng AB = OK.
c) Tìm điều kiện của hình thoi ABCD để OBKC là hình vuông.