Cho hình thang cân ABCD. Đáy nhỏ AB bằng cạnh bên BC và đường chéo AC vuông góc với cạnh bên AD.

a) Tính các góc của hình thang cân.

b) Chứng minh rằng trong hình thang cân đó đáy lớn gấp đôi đáy nhỏ.

Lời giải

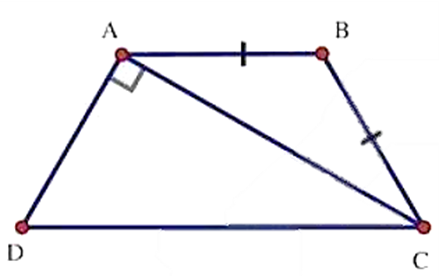
a) ABCD là hình thang cân \[ \Rightarrow \widehat D = \widehat C;\;\widehat A = \widehat B\].

• Xét ∆ACD có: \[\widehat {ADC} + \widehat {ACD} = 180^\circ - \widehat {DAC} = 180^\circ - 90^\circ = 90^\circ \]

• Xét ∆ABC có: AB = BC Þ ∆ABC cân tại B

\[ \Rightarrow \widehat {BAC} = \widehat {BCA}\]

Ta có: \[\widehat {DAB} = \widehat {DAC} + \widehat {CAB}\]

\[ = 90^\circ + \widehat {CAB} = \widehat {ADC} + \widehat {ACD} + \widehat {ACB}\]

\[ = \widehat {BCD} + \widehat {BCD} = 2\widehat {BCD}\]

Mà \(\widehat {DAB} + \widehat {BCD} = 180^\circ \Rightarrow 2\widehat {BCD} + \widehat {BCD} = 180^\circ \)

\( \Rightarrow 3\widehat {BCD} = 180^\circ \Rightarrow \widehat {BCD} = 60^\circ \)

\[ \Rightarrow \widehat C = \widehat D = 60^\circ \]

\[ \Rightarrow \widehat A = \widehat B = 180^\circ - \widehat C = 180^\circ - 60^\circ = 120^\circ \]

b) Xét ∆ADC có \(\widehat D = 60^\circ \Rightarrow \widehat {ACD} = 90^\circ - 60^\circ = 30^\circ \)

Trong một tam giác vuông, cạnh đối diện với góc 30° có độ dài bằng nửa cạnh huyền

Suy ra \(AD = \frac{1}{2}DC\).

Mà \(AD = BC = AB \Rightarrow AB = \frac{1}{2}DC\).