Cho hình thang cân ABCD, có đáy nhỏ và đường cao cùng bẳng 2a và \(\widehat {ABC} = 45^\circ \). Tính \(\left| {\overrightarrow {CB} - \overrightarrow {A{\rm{D}}} + \overrightarrow {AC} } \right|\).
A. \[a\sqrt 3 \]
B. \(2{\rm{a}}\sqrt 5 \)
C. \[{\rm{a}}\sqrt 5 \]
D. \[{\rm{a}}\sqrt 2 \].
Đáp án đúng là: B
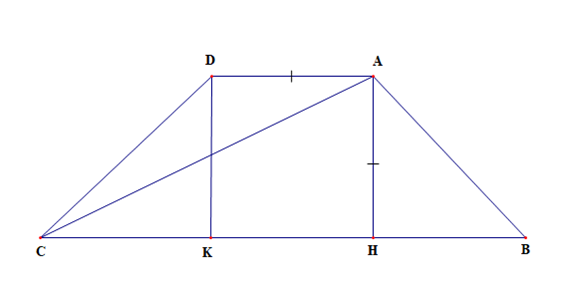
Gọi H, K là chân đường cao hạ từ A, D xuống BC
Khi đó tam giác ABH vuông tại H
Mà \(\widehat {ABC} = 45^\circ \)
Suy ra tam giác ABH vuông cân tại H
Do đó AH = BH = 2a
Vì hình thang ABCD cân
Nên AB = CD, \(\widehat {ABC} = \widehat {DCB}\), BD = AC
Xét tam giác ABH và tam giác DCK có
\(\widehat {AHB} = \widehat {DKC}\left( { = 90^\circ } \right)\)
AB = CD
\(\widehat {ABC} = \widehat {DCB}\)
Suy ra ∆ABH = ∆DCK (cạnh huyền – góc nhọn)
Do đó CK = BH = 2a
Ta có CH = AD + CK = 2a + 2a = 4a
Xét tam giac AHC vuông tại H có
AC2 = AH2 + CH2
Suy ra \[{\rm{AC = }}\sqrt {{{\left( {2{\rm{a}}} \right)}^2} + {{\left( {4{\rm{a}}} \right)}^2}} = 2{\rm{a}}\sqrt 5 \]
Ta có:
\(\left| {\overrightarrow {CB} - \overrightarrow {A{\rm{D}}} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} + \overrightarrow {DA} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} + \overrightarrow {DC} } \right| = \left| {\overrightarrow {DB} } \right| = AC = 2{\rm{a}}\sqrt 5 \)
Vậy ta chọn đáp án B.