Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần lượt là trung điểm của AB, CD và T là giao điểm của AC và BD (Hình 30). Chứng minh: a) ;
39
19/05/2024
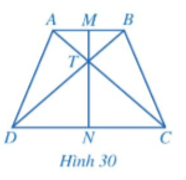
Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần lượt là trung điểm của AB, CD và T là giao điểm của AC và BD (Hình 30).
Chứng minh:
a) ;
Trả lời
a) Do ABCD là hình thang cân nên AC = BD và AD = BC (tính chất hình thang cân).
Xét ΔADC và ΔBCD có:
AD = BC; AC = BD; DC là cạnh chung
Do đó ΔADC = ΔBCD (c.c.c)
Suy ra (hai góc tương ứng)
Hay .
Chứng minh tương tự ta cũng có: ΔABD = ΔBAC (c.c.c)
Suy ra (hai góc tương ứng)
Hay .