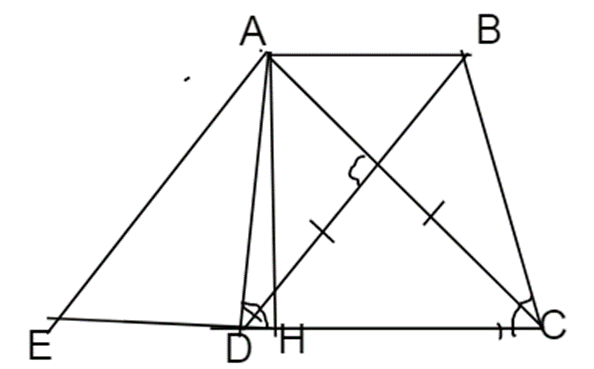
*Cách vẽ:

Nhận xét : Thang cân → 2 đường chéo bằng nhau. Gọi O là giao của 2 đường chéo,

hai đường chéo vuông góc → \(\Delta OCD\)vuông cân đỉnh O.

Vẽ: Vẽ tam giác vuông cân COD, trên tia đối của tia OC lấy A, trên tia đối của tia

OD lấy B sao cho OA = OB (< OC nếu AB là đáy nhỏ) → ABCD là thang cân đáy nhỏ AB, đáy lớn CD và có 2 đường chéo vuông góc.

*Tính AB + CD:

Từ A và B hạ AH và BK vuông góc CD, H, K thuộc CD. Do ABCD là thang cân đáy AB, CD

→ DH = CK và AB = HK

→ AB + CD = AB + DH + HK + KC = HK + CK + HK + KC = 2HC

\(\Delta OCD\) vuông cân đỉnh O \( \to \widehat {OCD} = {45^0} \to \widehat {ACD} = {45^0}\) lại có \(\Delta AHC\) vuông tại H, \(\widehat {ACD} = {45^0} \to \)vuông cân → HC = AH = h

→ tổng 2 đáy AB + CD = 2h