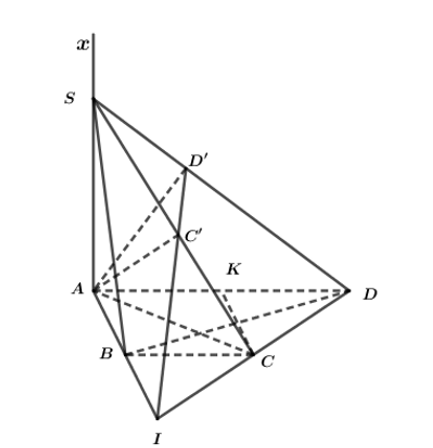
Cho hình thang ABCD vuông góc tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD. Chứng minh rằng $\widehat{SBC}=\widehat{SCD}=90°$.

Ta có: SA ^ BC; AB ^ BC

Þ SB ^ BC (định lý 3 đường vuông góc) hay $\widehat{SBC}=90°$.

Gọi K là trung điểm của AD ta có CK = AB = AD/2 nên tam giác ACD vuông tại C

Ta có: CD ^ AC; CD ^ SA

Þ CD ^ (SAC)

Dó đó CD ^ SC hay $\widehat{SCD}=90°$

Vậy $\widehat{SBC}=\widehat{SCD}=90°$