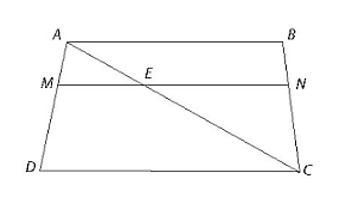
Cho hình thang ABCD (AB // CD) và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM = MD, 2BN = NC. Biết AB = 5 cm, CD = 6 cm, hãy tính độ dài đoạn thẳng MN.

Vẽ đường thẳng qua M song song với CD cắt AC tại E.

Khi đó: $\frac{AE}{EC}=\frac{AM}{MD}=\frac{1}{2}$ (định lí Thalès).

Do đó $\frac{AE}{EC}=\frac{BN}{NC}=\frac{1}{2}$ (2BN = NC), suy ra NE // AB (định lí Thalès đảo).

Ta có:

ME // CD

NE // AB

AB // CD

Do đó ME // CD và NE // CD, suy ra M, N, E thẳng hàng.

Mặt khác ∆AME ∽ ∆ADC (vì ME // CD).

Nên $\frac{ME}{DC}=\frac{AM}{AD}=\frac{1}{3}\Rightarrow ME=\frac{DC}{3}=\frac{6}{3}=2$ (cm).

Tương tự ∆CEN ∽ ∆CAB (vì NE //AB) nên $\frac{EN}{AB}=\frac{CN}{CB}=\frac{2}{3}\Rightarrow EN=\frac{2AB}{3}=\frac{10}{3}$ (cm).

Vậy MN = ME + EN = $\frac{16}{3}$ (cm).