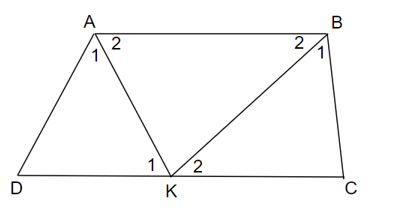
Cho hình thang ABCD (AB // CD). Hai đường phân giác của góc A và B cắt nhau tại điểm K thuộc đáy BC. Chứng minh AD + BC DC.
69
01/06/2024
Cho hình thang ABCD (AB // CD). Hai đường phân giác của góc A và B cắt nhau tại điểm K thuộc đáy BC. Chứng minh AD + BC = DC.
Trả lời
Vì AB // CD Þ ^A2=^K1 (hai góc so le trong)
Mà AK là phân giác của ^BAD⇒^A1=^A2
Do đó, ^A1=^K1 Þ ∆ADK cân tại D Þ AD = KD (1)
Ta lại có AB // CD ⇒^B2=^K2(hai góc so le trong)
Mà BK là phân giác của ^ABC⇒^B1=^B2
Do đó ^B1=^K2 Þ ∆BCK cân tại C Þ BC = KC (2)
Từ (1) và (2) Þ AD + BC = KD + KC.
Mặt khác K Î CD nên CD = KD + KC Þ CD = AD + BC (đpcm).