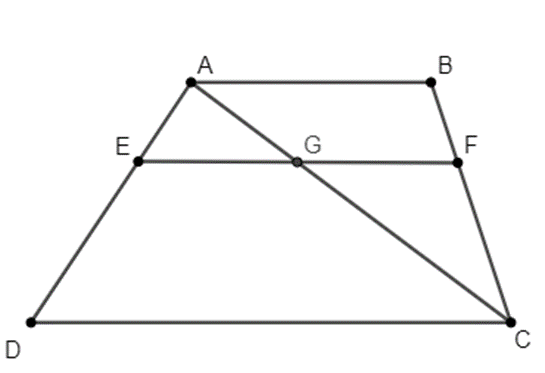
Cho hình thang ABCD (AB // CD) có BC = 15 cm. Điểm E thuộc cạnh AD sao cho $\frac{{AE}}{{AD}} = \frac{1}{3}$. Qua E kẻ đường thẳng song song với CD cắt BC tại F. Tính độ dài BF.

A. 10 cm;

B. 5 cm;

C. 11 cm;

D. 7 cm.

Đáp án đúng là: B

Gọi I là giao điểm của AC và EF.

Xét tam giác ACB có IF // AB nên theo định lý Ta−lét, ta có:

$\frac{{BF}}{{BC}} = \frac{{AI}}{{AD}} = \frac{1}{3}$ nên $BF = \frac{1}{3}BC = \frac{1}{3}.15 = 5$ (cm).