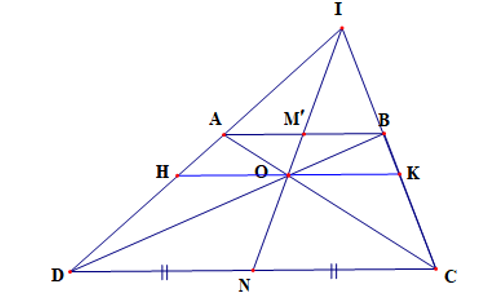
Cho hình thang ABCD (AB < CD), AD cắt BC tại I, AC cắt BD tại O. Gọi M, N lần lượt là trung điểm của AB, DC. Chứng minh rằng I, M, O, N thẳng hàng.

• Gọi M’ là giao điểm của IN và AB. Ta cần chứng minh M’ ≡ M.

Trong DIDN có AM’ // DN nên theo hệ quả định lí Thalès ta có: $\frac{A{M}^{\text{'}}}{DN}=\frac{I{M}^{\text{'}}}{IN}$

Trong DICN có BM’ // CN nên theo hệ quả định lí Thalès ta có: $\frac{B{M}^{\text{'}}}{CN}=\frac{I{M}^{\text{'}}}{IN}$

Suy ra $\frac{A{M}^{\text{'}}}{DN}=\frac{B{M}^{\text{'}}}{CN}\left(=\frac{I{M}^{\text{'}}}{IN}\right)$

Mà DN = CN nên AM’ = BM’ hay M’ là trung điểm của AB.

Do đó M’ ≡ M nên I, M, N thẳng hàng (*)

• Qua O kẻ đường thẳng song song với CD cắt ID và IC lần lượt tại H và K.

Trong DADC có HO // DC nên theo hệ quả định lí Thalès ta có:  $\frac{HO}{DC}=\frac{AO}{AC}$(1)

Trong DBDC có KO // DC nên theo hệ quả định lí Thalès ta có: $\frac{KO}{DC}=\frac{BO}{BD}$   (2)

Trong DODC có AB // DC nên theo hệ quả định lí Thalès ta có: $\frac{AO}{OC}=\frac{BO}{OD}$

Suy ra $\frac{AO}{AO+OC}=\frac{BO}{BO+OD}$  hay  $\frac{AO}{AC}=\frac{BO}{BD}$(3)

Từ (1), (2) và (3) suy ra $\frac{HO}{DC}=\frac{KO}{DC}$ , do đó HO = KO.

Chứng minh tương tự như trên ta có I, O, N thẳng hàng (**)

Từ (*) và (**) ta có I, M, O, N thẳng hàng.