b) Gọi O là tâm của tam giác đều A’BD. Hình chiếu vuông góc của ba đoạn AB, AD và AA’ lên (A’BD) có bằng nhau không?

c) Chỉ ra rằng $\widehat{BOD}=\widehat{DO{A}^{\text{'}}}=\widehat{A^{\text{'}}OB}=120°$.

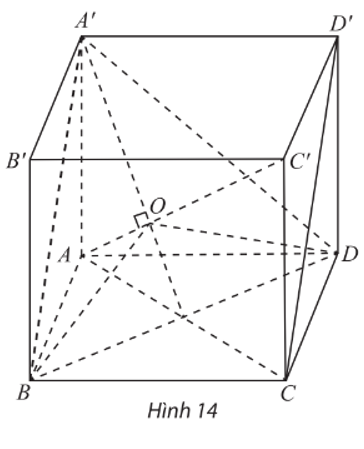
a) Ta có A’D ⊥ AD’ (AA’D’D là hình vuông) và A’D ⊥ C’D’ (C’D’ ⊥ (AA’D’D)).

Suy ra A’D ⊥ (AC’D’).

Do đó A’D ⊥ AC’   (1)

Chứng minh tương tự, ta được A’B ⊥ AC’   (2)

Từ (1), (2), ta thu được AC’ ⊥ (A’BD).

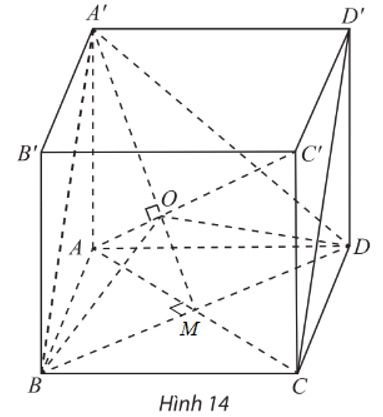
b) Gọi M là trung điểm BD.

Ta có AB = AD (do ABCD là hình vuông).

Suy ra tam giác ABD cân tại A.

Do đó AM ⊥ BD.

Lại có O là tâm của tam giác đều A’BD.

Suy ra A’M ⊥ BD và O ∈ A’M.

Ta có AM ⊥ BD và A’M ⊥ BD (chứng minh trên).

Suy ra BD ⊥ (AA’M).

Do đó BD ⊥ AO   (3)

Chứng minh tương tự, ta được A’D ⊥ AO   (4)

Từ (3), (4), suy ra AO ⊥ (A’BD).

Khi đó O là hình chiếu vuông góc của A lên mặt phẳng (A’BD).

Mà B là hình chiếu vuông góc của B lên mặt phẳng (A’BD).

Suy ra OB là hình chiếu vuông góc của AB lên mặt phẳng (A’BD).

Chứng minh tương tự, ta được: OD, OA’ lần lượt là hình chiếu vuông góc của AD, AA’ lên mặt phẳng (A’BD).

Tam giác A’BD đều có tâm O.

Suy ra OA’ = OB = OD.

Vậy hình chiếu vuông góc OB, OD và OA’ lần lượt của ba đoạn AB, AD và AA’ lên (A’BD) có độ dài bằng nhau.

c) Ta có tam giác A’BD đều. Suy ra $\widehat{B{A}^{\text{'}}D}=60°$.

Tam giác A’BD đều có tâm O. Suy ra O là tâm đường tròn ngoại tiếp tam giác A’BD.

Khi đó $\widehat{BOD}=2\widehat{B{A}^{\text{'}}D}=2.60°=120°$.

Chứng minh tương tự, ta được $\widehat{DO{A}^{\text{'}}}=120°$ và $\widehat{A^{\text{'}}OB}=120°$.

Vậy $\widehat{BOD}=\widehat{DO{A}^{\text{'}}}=\widehat{A^{\text{'}}OB}=120°$.