Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Tính khoảng
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Tính khoảng cách từ A đến mặt phẳng (A'BC).
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Tính khoảng cách từ A đến mặt phẳng (A'BC).
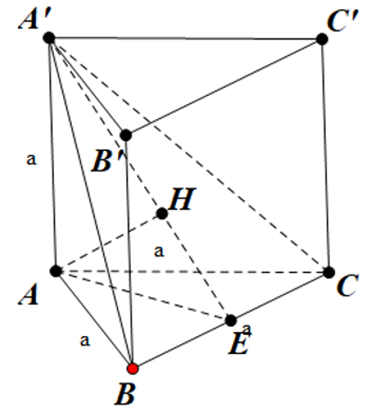
Gọi E là trung điểm của BC.
Ta có: {A′E⊥BCAE⊥BC⇒(A′AE)⊥(A′BC)
Kẻ đường cao AH (H Î A'E) Þ AH ^ (A'BC)
Þ d(A, (A'BC)) = AH
=√A′A2.AE2A′A2+AE2=√a2.(a√32)2a2+(a√32)2=a√217.
Vậy khoảng cách từ A đến mặt phẳng (A'BC) bằng a√217.