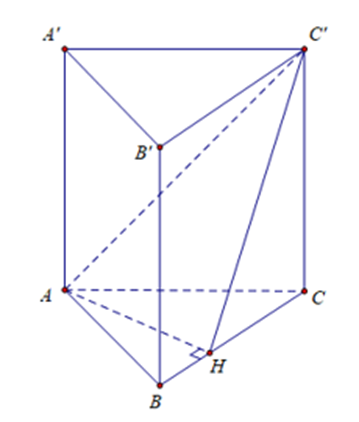
Gọi H là hình chiếu của A trên BC

Ta có AH ⊥ BC, AH ⊥ BB’ nên AH ⊥ (BCC’B’)

Suy ra HC’ là hình chiếu của AC’ trên mặt phẳng (BCC’B’)

Do đó góc giữa AC’ và mặt phẳng (BCC’B’) là góc \(\widehat {AC'H}\)

Vì tam giác ABC vuông tại A nên \[{{\rm{S}}_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\]

Vì tam giác ABC vuông tại A nên theo định lý Pytago có

\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {3{{\rm{a}}^2} + {a^2}} = 2{\rm{a}}\)

Suy ra \(AH = \frac{{AC.AB}}{{BC}} = \frac{{a\sqrt 3 .a}}{{2{\rm{a}}}} = \frac{{a\sqrt 3 }}{2}\)

Vì tam giác AA’C’ vuông tại A’ nên theo định lý Pytago có

\(AC' = \sqrt {AA{'^2} + A'C{'^2}} = \sqrt {{{\rm{a}}^2} + {a^2}} = \sqrt 2 {\rm{a}}\)

Xét tam giác AC’H có

\[\sin \widehat {AC'H} = \frac{{AH}}{{AC'}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{a\sqrt 2 }} = \frac{{\sqrt 6 }}{4}\]

Vậy ta chọn đáp án D.