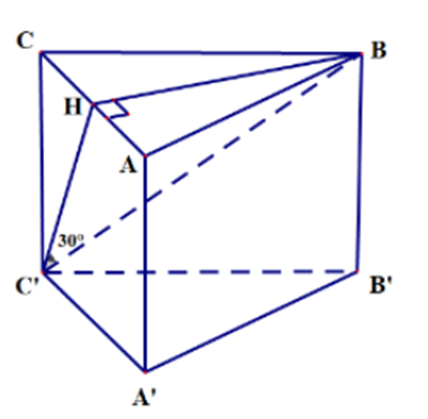
Cho hình lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a, đường thẳng BC’ tạo với mặt phẳng (ACC’A’) một góc 30°. Tính thể tích V của khối lăng trụ ABC.A’B’C’.
A. \(V = \frac{{\sqrt 6 }}{4}{a^3}\);
B. \(V = \frac{{{a^3}}}{8}\);
C. \(V = \frac{{\sqrt 3 }}{4}{a^3}\);
D. \(V = \frac{3}{8}{a^3}\).
Đáp án đúng là: A
Gọi H là trung điểm của AC.
Ta có: tam giác ABC là tam giác đều nên BH ⊥ AC.
Mà BH ⊂ (ABC) và (ABC) ⊥ (ACC’A’).
Do đó BH ⊥ (ACC’A’)
Lại có C’H ⊂ (ACC’A’) nên BH ⊥ C’H.
Suy ra góc giữa BC’ và (ACC’A’) là \(\widehat {BC'H}\)
Do đó \(\widehat {BC'H} = 30^\circ \).
Xét tam giác BHC’ vuông tại H có
\(C'H = \frac{{BH}}{{\tan 30^\circ }} = \frac{{a\sqrt 3 }}{2}:\frac{{\sqrt 3 }}{3} = \frac{{3{\rm{a}}}}{2}\)
Xét tam giác CHC’ vuông tại C có \(C'C = \sqrt {C'{H^2} - C{H^2}} = \sqrt {\frac{{9{{\rm{a}}^2}}}{4} - \frac{{{a^2}}}{4}} = a\sqrt 2 \)
Thể tích khối lăng trụ là
\(V = C'C.{S_{ABC}} = C'C.\frac{1}{2}.BH.AC = a\sqrt 2 .\frac{1}{2}.\frac{{a\sqrt 3 }}{2}.a = \frac{{\sqrt 6 }}{4}{a^3}\)
Vậy ta chọn đáp án A.