Cho hình hộp đứng ABCD.A'B'C'D' có đáy là hình vuông cạnh a góc giữa mặt phẳng (D'AB) và mặt phẳng (ABB'A') bằng 30°. Tính thể tích khối hộp ABCD.A'B'C'D'.

Trả lời

Lời giải

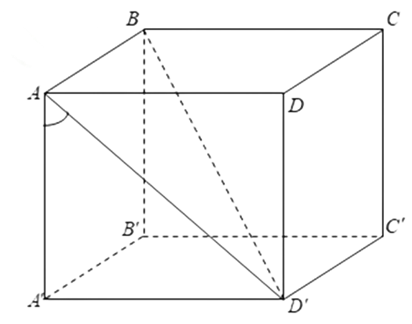
Ta có \[\left\{ \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {D'AB} \right) = AB\\\left( {ABB'A'} \right) \bot AB\end{array} \right.\] nên góc giữa mặt phẳng (ABB’A’) là góc giữa AD’ và AA’ hay \[\widehat {A'AD}\] = 30°

Suy ra \[AA' = \frac{{A'D'}}{{\tan 30^\circ }} = a\sqrt 3 \]

Ta có \[{S_{ABCD}} = a.a = {a^2}\].

Vậy thể tích hình hộp đứng ABCD.A'B'C'D' là:

V_{ABCD.A’B’C’D’} = AA’ . S_ABCD = \[{a^2}\,.\,a\sqrt 3 = {a^3}\sqrt 3 \] (đvtt).

Vậy thể tích hình hộp đứng ABCD.A'B'C'D' là \[{a^3}\sqrt 3 \] (đvtt).