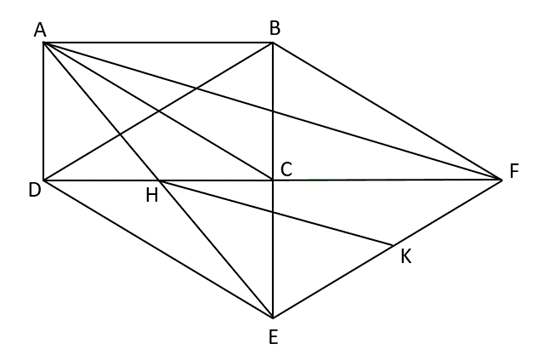
a) Xét tứ giác BDEF có:
C là trung điểm BF (E điểm đối xứng của B qua C)
C là trung điểm DF (F điểm đối xứng của D qua C)
Do đó tứ giác BDEF là hình bình hành
Mặc khác ABCD là hình chữ nhật nên BE ⊥ DF tại C
Vậy tứ giá BDEF là hình thoi.
b) Ta có: ABCD là hình chữ nhật có AC = BD;
BDEF là hình thoi (câu a) có BD = DE
Do đó AC = DE.
c) Ta có: ABCD là hình chữ nhật có AD = BC;
Mà BC = CE (E điểm đối xúng B qua C).
Do đó AD = CE.
Xét tứ giác ADEC có:
AC = DE (câu b)
AD = CE (cmt)
Do đó ADEC là hình hình hành.
Mà H là trung điểm cua CD nên H cũng là trung điểm của AE.
Xét ∆AEF có:
H là trng điểm của AE (cmt);
K là trung điểm của EF
⇒ HK là đường trung bình của ∆AEF nên HK // AF
d) Ta có: S∆AEF = S∆AHF + S∆HEF
\( \Leftrightarrow 30 = \frac{1}{2}AD\,.\,HF + \frac{1}{2}CE\,.\,HF\)
\( \Leftrightarrow \frac{1}{2}HF\left( {AD + CE} \right) = 30\)
\( \Leftrightarrow \frac{1}{2}.\frac{3}{2}CD\,.\,\left( {AD + AD} \right) = 30\)
\( \Leftrightarrow \frac{3}{2}CD\,.\,AD = 30\)
\[ \Leftrightarrow \frac{3}{2}\,.\,{S_{ABCD}} = 30\]
\( \Rightarrow {S_{ABCD}} = 30\,.\,\frac{2}{3} = 60\) (cm2).