Cho hình chữ nhật ABCD. Từ D hạ đường vuông góc với AC, cắt AC ở H. Biết rằng AB = 13 cm, DH = 5 cm. Tính BD.

Trả lời

Lời giải

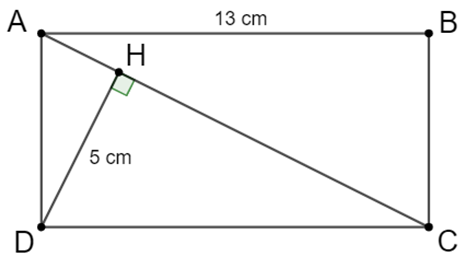
Áp dụng hệ thức lượng trong tam giác vuông vào ∆ADC vuông tại D có DH là đường cao.

$\Rightarrow \frac{1}{{D{H^2}}} = \frac{1}{{D{A^2}}} + \frac{1}{{D{C^2}}} \Leftrightarrow \frac{1}{{D{A^2}}} = \frac{1}{{D{H^2}}} - \frac{1}{{D{C^2}}}$

$\Leftrightarrow \frac{1}{{D{A^2}}} = \frac{1}{{{5^2}}} - \frac{1}{{{{13}^2}}} = \frac{{144}}{{4225}} \Rightarrow DA = \frac{{65}}{{12}}\;\,\,(cm)$.

Áp dụng định lí Pytago vào ∆ADC vuông tại D.

$\Rightarrow AC = \sqrt {A{D^2} + D{C^2}} = \sqrt {{{\left( {\frac{{65}}{{12}}} \right)}^2} + {{13}^2}} = \frac{{169}}{{12}}\;\,\,(cm)$.

Mà ABCD là hình chữ nhật nên suy ra: $BD = AC = \frac{{169}}{{12}}\;\,(cm)$.