Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính veco AB . vecto AO
Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính \(\overrightarrow {AB} \,.\,\overrightarrow {AO} \).
A. a;
B. 0;
C. a2;
D. 2a2.
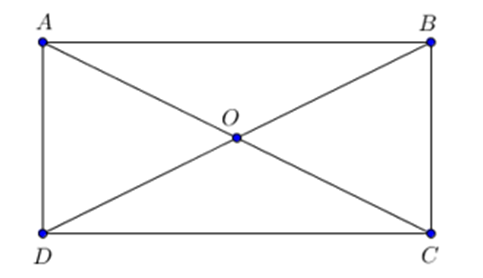
Ta có ABCD là hình chữ nhật có: BC = AD = a, AB = CD = 2a.
Xét ∆ABC vuông tại B có:
AC2 = AB2 + BC2 = (2a)2 + a2 = 5a2
\( \Rightarrow AC = a\sqrt 5 \)
Mà \(OA = \frac{1}{2}AC = \frac{{a\sqrt 5 }}{2}\)
Ta có: \(\left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) = \widehat {BAO} = \widehat {BAC}\)
\(\cos \widehat {BAC} = \frac{{AB}}{{AC}} = \frac{{2a}}{{a\sqrt 5 }} = \frac{{2\sqrt 5 }}{5}\)
Vậy \(\overrightarrow {AB} .\overrightarrow {AO} = \left| {\overrightarrow {AB} } \right|\left| {\overrightarrow {AO} } \right|\cos \left( {\overrightarrow {AB} ,\,\,\overrightarrow {AO} } \right) = 2a.\frac{{a\sqrt 5 }}{2}.\frac{{2\sqrt 5 }}{5} = 2{a^2}\).
Đáp án đúng là D.