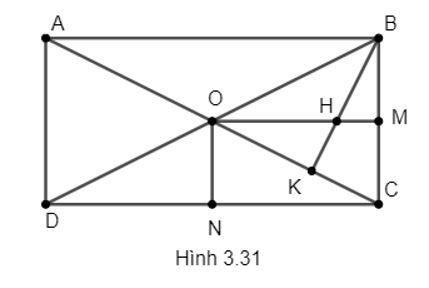
Cho hình chữ nhật ABCD. Gọi O là trung điểm của AC. Hạ OM vuông góc với BC tại M, ON vuông góc với BC tại N.
Cho hình chữ nhật ABCD. Gọi O là trung điểm của AC. Hạ OM vuông góc với BC tại M, ON vuông góc với BC tại N.
a) Chứng minh
b) Chứng minh MN = OC.
c) Kẻ BK vuông góc với AC tại K, OM giao với BK tại H. Chứng minh CH vuông góc với MB.