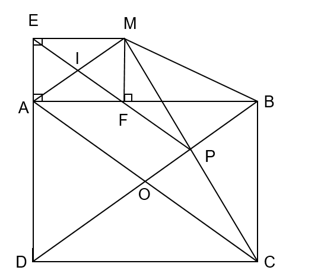
Cho hình chữ nhật ABCD đường chéo AC và BD cắt nhau tại O. Lấy P là điểm tùy ý trên OB. Gọi M là điểm đối xứng với C qua P. Từ M kẻ ME vuông góc với đường thẳng AB (F ∈ AB).

a) Chứng minh AEFM là hình chữ nhật.

a) Ta có:$\widehat{EAF}={90}^o$  (ABCD là hình vuông);  $\widehat{MEA}={90}^o$(ME vuông góc AD tại E);  $\widehat{EMF}={90}^o$ (MF vuông góc AB tại F).

⇒Tứ giác AEMF có 3 góc vuông nên AEMF là hình chữ nhật.