Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAD là tam giác đều và nằm
25
12/09/2024
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD (tham khảo hình vẽ bên). Tính bán kính R của khối cầu ngoại tiếp hình chóp S.CMN.
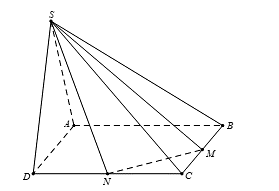
Trả lời
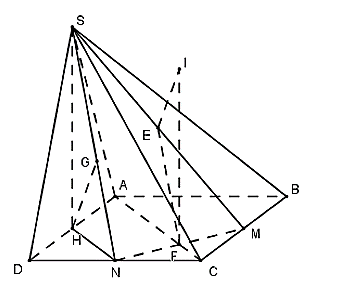
Gọi H là trung điểm của cạnh AB nên SH ^ AB
Mặt khác (SAB) ^ (ABCD) Þ SH ^ (ABCD)
Gọi F là trung điểm của MN, ΔCMN vuông tại C nên F là tâm đường tròn ngoại tiếp ΔCMN
Qua F kẻ d1 // SH Þ d1 ^ (ABCD)
Ta có:
+)
+)
+)
Suy ra SN2 + MN2 = SM2
Do đó tam giác SMN vuông tại N
Gọi E là trun điểm của SM, qua E kẻ d2 ^ (SMN) sao cho d2 Ç d1 = I là tâm mặt cầu ngoại tiếp chóp S.CMN.
Dễ thấy ΔHMN vuông cân tại N
Ta có:
Có EI ^ (SMN) Þ EI ^ EF
Do đó ∆EIF vuông tại E
.
Xét tam giác vuông SIE có:
.
Vậy bán kính R của khối cầu ngoại tiếp hình chóp S.CMN là: .


