Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a; SA = a căn bậc hai của 3; SA^ABCD. Gọi M, N lần lượt là trung điểm của SB; SD, mặt phẳng (AMN) cắt SC tại I. Tính thể tích của khối đa diệ
94
13/05/2024
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a; \(SA = a\sqrt 3 \); SA ^ (ABCD). Gọi M, N lần lượt là trung điểm của SB; SD, mặt phẳng (AMN) cắt SC tại I. Tính thể tích của khối đa diện ABCDMIN
Trả lời
Lời giải
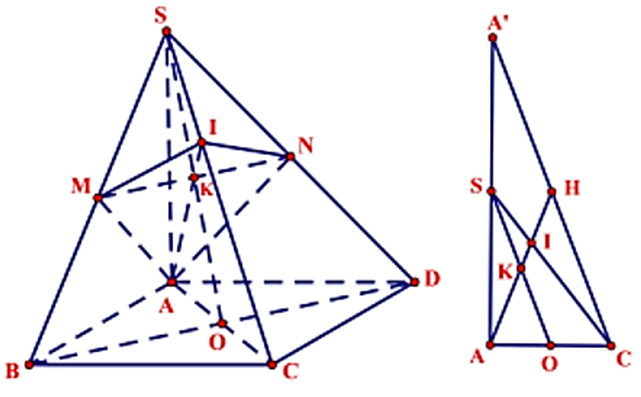
Gọi O là tâm hình vuông.
SO cắt MN tại K Þ I là giao điểm của AK với SC.
Vì MN là đường trung bình của tam giác SBD nên K là trung điểm của SO.
Gọi A' là điểm đối xứng của A qua S, H là giao điểm của AK và SC.
Vì SO // A'C và K là trung điểm của SO
Þ H là trung điểm của A'C
Þ I là trọng tâm của tam giác AA'C
\( \Rightarrow SI = \frac{1}{3}SC\)
Ta có:
• \({V_{S.ABCD}} = \frac{1}{3}SA.{S_{ABCD}} = \frac{{{a^3}\sqrt 3 }}{3}\);
• \({V_{S.ABD}} = {V_{S.}}_{BCD} = \frac{1}{2}{V_{S.}}_{ABCD}\).
Khi đó: \({V_{S.AMIN}} = {V_{S.AMN}} + {V_{S.MIN}}\)
\( = \frac{1}{1}.\frac{1}{2}.\frac{1}{2}.{V_{S.ABD}} + \frac{1}{2}.\frac{1}{2}.\frac{1}{3}.{V_{S.BCD}}\)
\( = \frac{1}{4}{V_{S.ABD}} + \frac{1}{{12}}{V_{S.BCD}} = \left( {\frac{1}{4} + \frac{1}{{12}}} \right).\frac{1}{2}{V_{S.ABCD}} = \frac{1}{6}{V_{S.ABCD}}\).
Do đó: \({V_{ABCDMIN}} = {V_{S.ABCD}} - {V_{S.AMIN}} = \frac{5}{6}{V_{S.ABCD}} = \frac{{5{a^3}\sqrt 3 }}{{18}}\).

