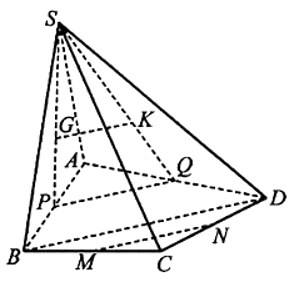
Cho hình chóp tứ giác S.ABCD. Gọi G, K lần lượt là trọng tâm của các tam giác SAB và SAD; M, N lần lượt là trung điểm của BC và CD. Chứng minh rằng GK // MN.
Cho hình chóp tứ giác S.ABCD. Gọi G, K lần lượt là trọng tâm của các tam giác SAB và SAD; M, N lần lượt là trung điểm của BC và CD. Chứng minh rằng GK // MN.