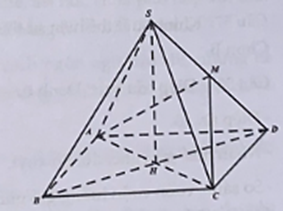
Cho hình chóp tứ giác đều S.ABCD có thể tích . Gọi M là trung điểm cạnh SD. Nếu  thì khoảng cách d từ  đến mặt phẳng (MAC) bằng bao nhiêu?

Trả lời

Đáp án: 0,5

Gọi H là tâm hình vuông $\text{ABCD}\Rightarrow \text{SH}\perp \left(\text{ABCD}\right)$

Đặt $AB=a(a>0).S_{ABCD}=a^2;BD=a\sqrt{2}$.

Tam giác SBD vuông tại S nên $\text{SH}=\frac{\text{a}\sqrt{2}}{2}$.

${\text{V}}_{\text{S}.\text{ABCD}}=\frac{1}{3}\text{SH}\cdot {\text{S}}_{\text{ABCD}}=\frac{\sqrt{2}}{6}{\text{a}}^3=\frac{\sqrt{2}}{6}\Rightarrow \text{a}=1.$

${\text{V}}_{\text{MACD}}=\frac{1}{4} {\text{V}}_{\text{S.ABCD}}=\frac{\sqrt{2}}{24};\text{HM}=\frac{1}{2}\text{SB}=\frac{1}{2}$ (Vì SB = AB = 1)

${\text{S}}_{\text{MAC}}=\frac{1}{2}\text{MH.AC}=\frac{1}{2}.\frac{1}{2}.\sqrt{2}=\frac{\sqrt{2}}{4}.$ Ta có $\text{d}(\text{B},(\text{MAC}\left)\right)=\text{d}(\text{D},(\text{MAC}\left)\right).$

Lại có: ${\text{V}}_{\text{MACD}}=\frac{1}{3}.d(D,(MAC\left)\right).S_{MAC}\Rightarrow d(D,(MAC\left)\right)=\frac{3 {\text{V}}_{\text{MACD}}}{S_{MAC}}=\frac{1}{2}$.