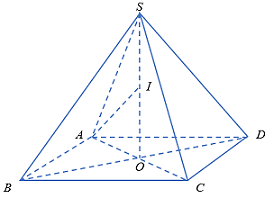
ABCD là hình chữ nhật tâm O suy ra: OA = OB = OC = OD

Lại có: SA = SB = SC = SD

Suy ra SO ^ (ABCD)

Þ SO ^ OC

Xét ΔSOC vuông tại O có: SC² = SO² + OC²

Þ OC² = SC² − SO² = 5a² − 3a² = 2a²

 $\Rightarrow OC=a\sqrt{2}\Rightarrow AC=2.OC=2a\sqrt{2}$

Ta có:  $\sin \widehat{CAD}=\frac{CD}{AC}\Rightarrow CD=AC.\sin \widehat{CAD}=2a\sqrt{2}.\sin 30°=a\sqrt{2}$

Lại có:  $\cos \widehat{CAD}=\frac{AD}{AC}\Rightarrow AD=AC.\cos \widehat{CAD}=2a\sqrt{2}.\cos 30°=a\sqrt{6}$

Suy ra  $S_{ABCD}=AD.CD=a\sqrt{2}.a\sqrt{6}=2a^2\sqrt{3}$

Vậy thể tích của hình chóp S.ABCD là:

 $V_{S.ABCD}=\frac{1}{3}SO.S_{ABCD}=\frac{1}{3}.a\sqrt{3}.2a^2\sqrt{3}=2a^3$.