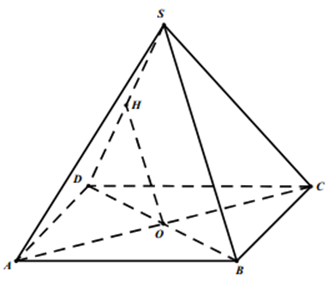
Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng 1, $\text{SD}=\sqrt{2},\text{SA}=\text{SB}=1$, và mặt phẳng (SBD) vuông góc với (ABCD). Tính khoảng cách giữa hai đường thẳng AC và SD. (kết quả làm tròn đến hàng phần chục.)

Theo giả thuyết $\left(\text{ABCD}\right)\perp \left(\text{SBD}\right)$ theo giao tuyến BD.

Do đó nếu dựng $\text{AO}\perp \left(\text{SBD}\right)$ thì $\text{O}\in \text{BD}$.

Mặt khác $\text{AS}=\text{AB}=\text{AD}\Rightarrow \text{OS}=\text{OB}=\text{OD}$ hay $\Delta \text{SBD}$ là tam giác vuông tại S

$\begin{array}{l}\text{BD}=\sqrt{{\text{SB}}^2+{\text{SD}}^2}=\sqrt{1^2+2}=\sqrt{3}\\ \text{AO}=\sqrt{{\text{AB}}^2-{\text{OB}}^2}=\sqrt{1^2-\frac{3}{4}}=\frac{1}{2}\end{array}$

Trong $\Delta \text{SBD}$ dựng $\text{OH}\perp \text{SD}$ tại $\text{H}\left(1\right)\Rightarrow \text{H}$ là trung điểm của SD.

Theo chứng minh trên $\text{AO}\perp \left(\text{SBD}\right)\Rightarrow \text{OA}\perp \text{OH}\left(2\right)$

Từ (1) và (2) chứng tỏ OH là đoạn vuông góc chung của AC và SD.