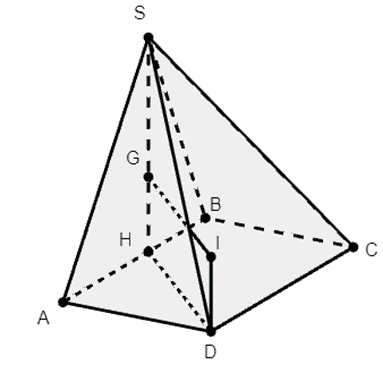
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(\widehat {ABC} = 120^\circ \); ∆SAB đều và nằm trong mặt phẳng vuôn góc với mặt đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng
A. \(\frac{{a\sqrt {11} }}{6}\);
B. \(\frac{{a\sqrt {39} }}{6}\);
C. \(\frac{{a\sqrt {37} }}{6}\);
D. \(\frac{{a\sqrt {35} }}{6}\).
Đáp án đúng là: B
Gọi H là trung điểm của AB, khi đó SH ⊥ AB
Lại có (SAB) ⊥ (ABCD) suy ra SH ⊥ (ABCD)
Ta có: \(\widehat {ABC} = 120^\circ \Rightarrow \widehat {BAD} = \widehat {BCD} = 60^\circ \)
Suy ra, tam giác BAD; BCD là tam giác đều.
Do đó DA = DB = DC.
Khi đó, D là tâm đường tròn ngoại tiếp tam giác ABC.
Vì tam giác SAB; ABD là tam giác đều nên DH ⊥ (SAB)
Trục đường tròn ngoại tiếp tam giác SAB cắt đường thẳng Dt (Dt // SH) tại I nên I là tâm mặt cầu ngoại tiếp khối chóp S.ABC.
Ta có: \(DH = \frac{{a\sqrt 3 }}{2} = IG\); \(SG = \frac{2}{3}SH = \frac{{a\sqrt 3 }}{3}\)
\( \Rightarrow R = \sqrt {I{G^2} + S{G^2}} = \frac{{a\sqrt {39} }}{6}\).