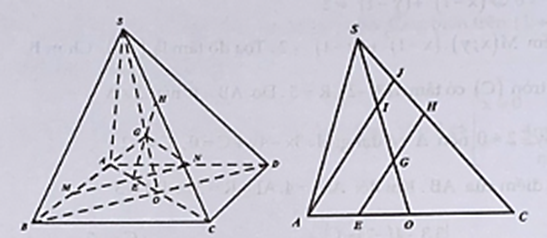Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, AD và G là trọng tâm tam giác SBD. Mặt phẳng (MNG) cắt SC
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, AD và G là trọng tâm tam giác SBD. Mặt phẳng (MNG) cắt SC tại điểm H. Tính SHSC
A. 25
B. 14
C. 13
D. 23